The term Ambit Stochastics indicates a broad field of mathematical research with applications in a wide range of subject areas belonging to natural science, economics, and biology/medicine. A brief introduction to the basics of ambit stochastics can be found in the adduced selected references. Further references are given in the individual sections under Research.
Key examples of applications are to the modelling of turbulent flows, the modelling of financial energy markets and the modelling of biological growth.
Ambit Stochastics deals with the study of random objects whose properties depend on time and spatial position (or any other type of variables). The variability in space and time is controlled through specific regions in space and time, the so-called ambit sets, and encompasses additional basic stochastic variation, the so-called intermittency/volatility.
This approach is very general and comprises in particuar the basic idea of a causality cone in the past that is fundamental in physics. Accordingly, Ambit Stochastics has the potiential to be applied in many fields of sciences where the variability at a certain point can be partly traced back to what happened in a region associated to this point.
The initialising example for the application of Ambit Stochastics to real phenomena is turbulence. Over the past few years a unifying modelling framework has been developed that is able to capture the main stylized features of turbulent flows. The mathematical research in this direction has matured to a stage where more extensive data acquisition, analysis and comparison is called for. This constitutes an exciting interplay between theory and experiment, typical for the development of the whole field of Ambit Stochastics.
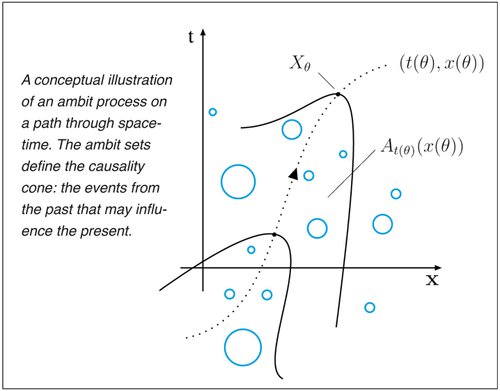
The term ambit originates from the latin words ambire, ambitus which denotes the border, boundary or sphere of influence. Ambit sets are the regions of influence in the past.