The core of ambit stochastics is mathematical, consisting in the study and development of certain types of stochastic (probabilistic) structures, more specifically stochastic fields and tempo-spatial stochastic processes embedded in such fields. More precisely still, the fields and processes in question have the special character of incorporating concrete specifications of the regions in space-time that influence the dynamic development - the ambit regions - and also the type of latent random variations that go byond the most basic stochastic innovations and are known as volatility or intermittency.
Ambit fields in space and time have the general form
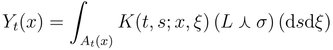
where ![]() denotes time,
denotes time, ![]() denotes position,
denotes position, ![]() is a deterministic kernel,
is a deterministic kernel, ![]() is a positive random field, and
is a positive random field, and ![]() denotes a subordinated Lévy basis (an independently scattered infinitely divisible random measure). The domain of integration
denotes a subordinated Lévy basis (an independently scattered infinitely divisible random measure). The domain of integration ![]() is the associated ambit set, attached to the point
is the associated ambit set, attached to the point ![]() and the stochastic field
and the stochastic field ![]() represents the volatility/intermittency.
represents the volatility/intermittency.
Particular specifications of the above formula find applications in various research areas like turbulence, economics and biology.
The AHOI Network
To further the development of Ambit Stochastics and its applications a research network with acronym AHOI has recently been created.
AHOI (Aarhus, Heidelberg, Oslo, Imperial) is a collaborative network between researchers in Stochastics at the Thiele Centre, Department of Mathematics, Aarhus University; Center for Research in Econometric Analysis of Time Series (CREATES), Department of Economics and Business, Aarhus University; Institute of Applied Mathematics. Heidelberg University; Centre of Mathematics for Applications (CMA), Department of Mathematics, Oslo University; and Department of Mathematics, Imperial College, London. The AHOI network, established in 2011, expects to be able over the next coming years to announce a number of postdoc positions internationally.
For further information see sites.google.com/site/ahoinet/