Ambit stochastics has a strong potential for applications in economics and finance. In particular, there are two important research areas which are currently being addressed:
Ambit fields are certain types of random fields which typically depend on both a temporal and also on a spatial variable. However, in the absence of a spatial component, we are in the so-called null-spatial case of an ambit field. In that situation, the random field simplifies to a stochastic process defined as a Lévy-driven, volatility modulated Volterra process:
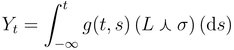
where ![]() is a subordinated Lévy process and g is a deterministic kernel function. Clearly, some regularity conditions are needed to ensure the existence of the integral.
is a subordinated Lévy process and g is a deterministic kernel function. Clearly, some regularity conditions are needed to ensure the existence of the integral.
An important sub-class of the above process is the class of Lévy semistationary (LSS) processes which is obtained by choosing a kernel function g which depends on t and s only through their difference, i.e.
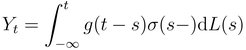
Then as soon as the stochastic volatility processes ![]() is stationary, the LSS process is itself a stationary process. Note that LSS processes form a very general class for modelling time series in continuous time since they can allow for a great variety of properties such as stochastic volatility, jumps, long memory and (semi)-heavy tailed distributions. Examples of LSS processes are Ornstein-Uhlenbeck (OU) and continuous-time autoregressive moving average (CARMA) processes.
is stationary, the LSS process is itself a stationary process. Note that LSS processes form a very general class for modelling time series in continuous time since they can allow for a great variety of properties such as stochastic volatility, jumps, long memory and (semi)-heavy tailed distributions. Examples of LSS processes are Ornstein-Uhlenbeck (OU) and continuous-time autoregressive moving average (CARMA) processes.
Current research in this area focuses in particular on modelling energy spot prices by LSS processes.
While applications of truly tempo-spatial ambit fields are quite natural in e.g. physics and biology, it might not be immediately clear, how such tempo-spatial models can be useful in economics or finance.
However, an area of current research addresses the questions of how to model the term structure of interest rates and how to describe the behaviour of forward or futures contracts.
Note that such contracts depend on at least two time dimensions: the current time and the time to maturity/delivery. In addition, e.g. commodity forwards typically also depend on the length of the delivery period.